B

 B. Operasi Pengurangan Bilangan Biner

Operasi aritmatika pengurangan pada bilangan biner juga sama seperti operasi pengurangan pada bilangan desimal, sebagai contoh perhatikan operasi dasar pengurangan bilangan biner berikut ini.

0 – 0 = 0
1 – 0 = 1
0 – 1 = 1 → bit ‘0’ meminjam 1 dari bit di sebelah kiri-nya
1 – 1 = 0

Contoh: Pengurangan 37 - 17 = 20 (desimal) atau 100101 - 010001 = 010100 (biner)

 1 → pinjam
100101 = 37
010001 = 17
-----------(-)
010100 = 20

Untuk menyatakan suatu bilangan desimal yang bernilai negatif adalah dengan menambahkan tanda negatif (-) pada bilangan-nya, contoh -1, -2, -3, -4, -5 dan seterusnya. Tetapi pada bilangan biner ini tidak bisa dilakukan, lalu bagaimana untuk membuat atau membedakan suatu bilangan biner itu bernilai negatif (-).

Ada beberapa cara untuk membuat suatu bilangan biner bernilai negatif, cara yang pertama adalah dengan menambahkan ekstra bit pada bagian paling sebelah kiri bilangan (Most Significant Bit / MSB), contoh;

101 = +5
Dengan menambahkan ekstra bit:
0101 = +5 → 0 merupakan ekstra bit (MSB) untuk tanda positif (+)
1101 = -5 → 1 merupakan ekstra bit (MSB) untuk tanda negatif (-)

Cara seperti di atas ternyata dapat menimbulkan salah persepsi jika kita tidak cermat, karena nilai -5 = 1101, 1101 dapat diartikan juga sebagai bilangan 13 dalam bilangan desimal. Maka digunakan cara kedua yaitu menggunakan satu metode yang dinamakan ‘Komplemen Dua’. Komplemen dua merupakan komplemen satu (yaitu dengan merubah bit ‘0’ menjadi ‘1’ dan bit ‘1’ menjadi ‘0’) kemudian ditambah satu, contoh :

0101 = +5 → ubah ke bentuk komplemen satu
1010 → komplemen satu dari 101 ini kemudian ditambahkan 1
   1
----(+)
1111 → ini merupakan bentuk komplemen dua dari 0101 yang bernilai -5

Contoh lain, berapakah nilai -7 pada bilangan biner?

0111 = +7
1000 → bentuk komplemen satu
   1
----(+)
1001 → bentuk komplemen dua dari 0111 yang bernilai -7

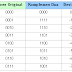
Berikut tabel dari perbandingan bilangan biner original dengan bilangan biner dalam bentuk komplemen dua.

Sedangkan contoh untuk operasi pengurangan menggunakan metode komplemen dua sebenarnya adalah operasi penjumlahan bilangan biner, perhatikan contoh berikut.

Contoh; hasil penjumlahan +6 + (– 4) = 2 (desimal), bagaimana jika dalam operasi penjumlahan bilangan biner (komplemen dua)?

Jawab: Pertama kita cari bentuk komplemen dua dari +4

0100 = +4
1011 → komplemen satu dari 1100
   1
----(+)
100 → komplemen dua dari 100

Lalu jumlahkan +6 = 110 dengan -4 = (100)

110
100
---(+)
010 = +2 → hasil penjumlahan 110 (+6) dengan 100 (-4)

Yang perlu diperhatikan dari operasi pengurangan bilangan biner menggunakan metode komplemen dua adalah jumlah bit-nya. Pada contoh di atas semua operasi pengurangan menggunakan bilangan biner 3 bit (bit = binary digit), maksudnya disini adalah jika bilangan biner yang dihitung merupakan bilangan biner 3 bit maka hasilnya harus 3 bit. Seperti pada pengurangan 110 dengan 100 dimana pada digit paling sebelah kiri (MSB) pada kedua bilangan biner yakni ‘1’ dan ‘1’ jika dijumlahkan hasilnya adalah ‘10’ tetapi hanya digit ‘0’ yang digunakan dan digit ‘1’ diabaikan.

1
 110
 100
----(+)
1010 → ‘1’ pada MSB diabaikan pada operasi pengurangan biner komplemen dua

Contoh lain hasil pengurangan bilangan desimal 3 – 5 = -2 jika dalam biner.

11
011 → bilangan biner +3
011 → komplemen dua bernilai -5
---(+)
110 → hasilnya = -2 (komplemen dua dari +2)

Untuk mengetahui apakah 110 benar-benar merupakan nilai komplemen dua dari +2 cara-nya sama seperti kita merubah dari biner positif ke biner negatif menggunakan metode komplemen dua. Perhatikan operasi-nya berikut ini.

110 = -2
001 → komplemen satu dari 110
  1
---(+)
010 → komplemen dua dari 110 yang bernilai +2

Dari contoh semua operasi perhitungan di atas dapat ditarik kesimpulan bahwa komplemen dua dapat digunakan untuk mengetahui nilai negatif dan nilai positif pada operasi pengurangan bilangan biner.